2015渋谷幕張中算数大問２(2)(3)をMathematicaで検算

昨年より全般に難しかった渋谷幕張の算数。本問を書き出しで正解出来た少年少女には頭が下がります。いやほんと。それな^^;

【問題】
図1のように，6 つの座席①，②，...，⑥と「待機場所」があり，座席にA，B，C，D，E，Fの6人が座っています。

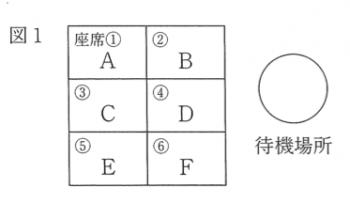
次のような［約束］で移動をくり返して席がえをします。ただし，席がえ後，もとの座席と同じ座席に座っている人がいてもよいことにします。

［約束］
・座席または「待機場所」のうち，空いているところへ1 人移動します。
・向じ人が続けて移動することはできません。

なお，移動の回数を数えるときは，「待機場所」への移動も「待機場所」から空いた座席への移動もそれぞれ1 回と数えることにします。
次の各問いに答えなさい。

(1)略
(2)図1 の座席から，ちょうど4 回の移動で席がえが終わりました。考えられる新しい座席は何通りですか。
(3)図1 の座席から席がえが終わるまで，移動の回数が最も少なくなる場合で6 回になるような新しい座席は何通り考えられますか。

【解答】
　　(以下で$m_n$はモンモール数(攪乱数列の総数) ，$m_1=0, m_2=1, m_3=2, m_4=9, m_5=44,...$を表します。)

(1) $4$回移動すると，$3$人の座席が入れ替わるので，$3$人の選び方$\times$入れ替わり方を計算する。
$${}_6C_3\times m_3=40\text{(通り)}$$
(3) $3$回の移動で2人ずつの座席が入れ替わるか，または$6$回の移動で$5$人の座席が入れ替わると考えるが，
　　$5$人が，$2$人，$3$人それぞれの間で入れ替わっているものは，$7$回かかるので，省かなければいけない。
$${}_6C_2\times m_2\times m_2\times {}_4C_2\times\frac12+ {}_6C_1\times (m_5-m_2\times m_3\times{}_5C_2)=189\text{(通り)}$$

【Mathematicaでブルートフォース検算】

A，B，C，D，E，Fには$n=$$1$〜$6$の番号を与え，待機場所は$x$とすると，交換の対象をリスト$\{1,2,3,4,5,6,x\}$で表せる。
1回の移動は，$n$と$x$の交換だと考えられるので，そういう交換を連ねた順列を用意する。
ただし，同じ交換が2度つづくものは省いておく。
交換の順列をリスト$\{1,2,3,4,5,6,x\}$に次々に適用し，第7要素が$x$であるものだけを取り出し，重複を省いて並べる。
$xlist$…4回交換後のリストのリスト
$ylist$…6回交換後のリストのリスト
$zlist$…1〜5回交換後のリストのリスト
(1)は$xlist$の要素数を数えれば好い
(2)は$ylist$から$zlist$と共通のものを省いたあとの要素数を数えれば好い


ClearAll["Global`*"];
xlist={};
xch=Range[1,6];
xchs=Tuples[xch,4];
xchs=DeleteCases[xchs,{___,a_,a_,___}];
For[i=1,i<= Length[xchs],i++,
y={1,2,3,4,5,6,x};
For[j=1,j<= Length[xchs[[i]]],j++,
y=y/.{xchs[[i,j]]->x,x-> xchs[[i,j]]}
];
xlist=Append[xlist,y];
]
xlist=Cases[xlist,{__,x}]//DeleteDuplicates;

ylist={};
xch=Range[1,6];
xchs=Tuples[xch,6];
xchs=DeleteCases[xchs,{___,a_,a_,___}];
For[i=1,i<= Length[xchs],i++,
y={1,2,3,4,5,6,x};
For[j=1,j<= Length[xchs[[i]]],j++,
y=y/.{xchs[[i,j]]->x,x-> xchs[[i,j]]}
];
ylist=Append[ylist,y];
]
ylist=Cases[ylist,{__,x}]//DeleteDuplicates;

zlist={};
xch=Table[Range[1,6],{k,1,5}]//Flatten;
xchs=Permutations[xch,5];
xchs=DeleteCases[xchs,{___,a_,a_,___}];
For[i=1,i<= Length[xchs],i++,
y={1,2,3,4,5,6,x};
For[j=1,j<= Length[xchs[[i]]],j++,
y=y/.{xchs[[i,j]]->x,x-> xchs[[i,j]]}
];
zlist=Append[zlist,y];
]
zlist=Cases[zlist,{__,x}]//DeleteDuplicates;

Print["(2)",Length[xlist],"通り"]
Print["(3)",Length[ylist]-Length[ylist\[Intersection]zlist],"通り"]


(2)40通り
(3)189通り